《Attention Is All You Need》精读报告

由于本人接触深度学习领域不久,仍有许多概念无法理解,希望各位多多指教。本篇报告主要在对论文原著以个人理解进行翻译的基础上进行补充说明,因此在包含论文原著内容的同时也会有本人的理解和对其他相关资料的引用补充
本论文是 Transformer 模型的首次提出,这篇文章最开始是 Google Brain 团队为了改善 Google Translate 的效果而发起的研究项目
Abstract
主流的序列转导模型:RNN(循环神经网络 - Recurrent Neural Network)、CNN(卷积神经网络 - Convolutional Neural Networks)
- 序列转录模型(sequence transduction model):给定一个序列,生成另外一个序列
- 基于编码器-解码器架构,通过注意力机制(attention)连接
提出 Transformer 架构:仅仅基于注意力机制,不使用循环和卷积,在多个翻译任务上取得较高的BLEU成绩
- BLEU:双语替换评测(bilingual evaluation understudy),用于评估模型生成的语句品质,通常将模型生成语句和人工翻译语句进行比较,通过计算两个语句的N-grams模型并统计匹配个数来得到结果。
双语替换评测的输出分数始终为0到1之间的数字。该输出值意味着候选译文与参考译文之间的相似程度,越接近1的值表示文本相似度越高。人工翻译少有能达到数值1,因为数值1表示候选文本与参考文本完全相同。—— Wikipedia
Intruduction
循环神经网络已被确认为序列建模和转导问题的先进方法
- 特别提及了 LSTM(长短期记忆 - long short-term memory)和GRNN(门控循环神经网络 - gated recurrent neural networks)
递归模型在推理时顺着输入输出序列的符号位置进行因子计算。在计算过程中,将符号的位置与步骤对齐(Aligning the positions to steps in computation time),并以此生成一个隐藏状态
- 换句话说,
是一个递归函数,接受 和t作为参数 - 按我的理解:递归模型顺着输入输出序列的符号位置进行因子计算指输入序列中元素的顺序就代表了因子计算的顺序 —— 如果将输入输出序列(一个测试样例)理解为一个数组的话,那么因子计算就是在对该数组进行正向遍历,从而就有了位置与步骤对齐
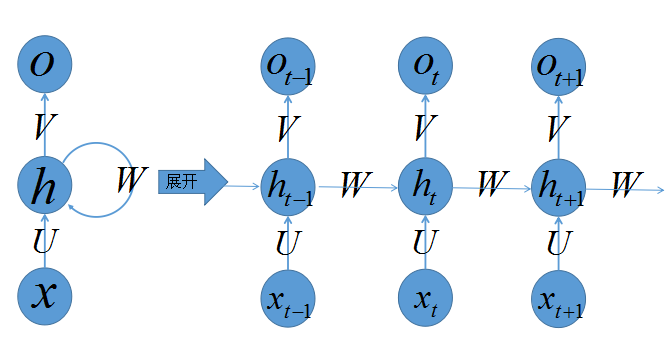
- t代表时间步,即计算的顺序
- h代表隐藏层 —— 神经网络中的参数
- x和o代表输入和输出
- w、u和v代表权重
递归函数限制了训练样本的并行化(递归本身需要上一个状态函数,只能线性进行)
- 在长序列的训练中,考虑到内存大小限制了批处理的规模,并行化尤为重要(This inherently
sequential nature precludes parallelization within training examples, which becomes critical at longer
sequence lengths, as memory constraints limit batching across examples.) - 最近的研究中通过因数分解和条件计算改进了计算效率,但仍然存在顺序计算的约束
注意力机制在过去就已经是序列转导的组成部分了,它允许对依赖关系进行建模,而不需要考虑它们在序列中的位置距离(allowing modeling of dependencies without regard to their distance in
the input or output sequences)
基于这点,作者引出了 Transformer 模型 —— 一种规避了递归算法,完全依赖于注意力机制来描绘输入和输出之间全局依赖关系的模型
- Transformer 模型显著地提高了并行度,并取得了较好的翻译效果
这一章主要提到了当前主流神经网络模型在并行性上存在的限制,由于使用了递归模型,不得不按照序列顺序计算隐藏状态,难以通过并行计算提升训练效率。在这种情况下,由于注意力机制不需要考虑序列中的位置距离就可以对远距离依赖关系进行建模,作者考虑到直接抛弃传统的递归模型,只依靠注意力机制来建立输入和输出之间的全局依赖关系,从而引出了本篇文章的核心 —— Transformer 模型。
Background
减少序列化的计算也是 Extended Neural GPU、ByteNet 和 ConvS2S 等模型的目标,这些模型采用了卷积神经网络(CNN)作为基础块,对所有输入输出序列的位置计算其隐藏表示
- 对于将任意两个位置的输入/输出信号建立联系需要的操作次数和这两个信号在序列中的位置距离的关系(the number of operations required to relate signals from two arbitrary input or output positions grows in the distance between positions):ConvS2S 是线性增长的;而 ByteNet 是对数增长的
- 基于上一点,导致这些模型在学习远距离的依赖关系时较为困难
存疑:什么是有效分辨率?
在 Transformer 模型中,操作次数被简化到了常数级 —— 代价是由于平均注意力加权位置导致的有效分辨率降低(albeit at the cost of reduced effective resolution due
to averaging attention-weighted positions)
- 在3.2章节中提到了通过多头注意力的解决方案
Self-Attention(a.k.a Intra-Attention):一种将单序列中不同位置联系起来,以计算序列表示的注意力机制
- 端到端记忆神经网络基于递归注意力机制而非序列对齐递归(即上文Introduction一章中提到的)
- 端到端指神经网络可以直接利用输入的数据,而不需要经过其他预处理(如标记等)
- Transfomer 模型是第一个完全依赖于自注意力机制而不使用 RNN 和 CNN(这两个使用的是序列对齐递归)的模型
这一章对上一章中提到的计算远距离依赖关系这一点进行了展开。由于传统的神经网络模型都需要考虑到序列中的位置关系,不得不对序列遍历处理,因此复杂度均不低于线性(
Model Architecture
大多数竞争性(competitive,这里指的应该是有竞争力的意思)的神经序列转导模型都采用了编码器-解码器架构
- 编码器(encoder): 它接受一个长度可变的序列作为输入, 并将其转换为具有固定形状的编码状态。
- 解码器(decoder): 它将固定形状的编码状态映射到长度可变的序列。
编码器将一组符号表示的输入序列
Transformer 模型整体架构遵循了基于多重堆叠的自注意力、逐点(Point-Wise)、完全连接的编码器/解码器层的设计
- Point-wise 操作主要指在计算机编程、尤其是在处理数组、矩阵或高维数据时,对数据的每个元素单独执行的操作。
在数学中,限定词逐点(英语:Pointwise)用于表明考虑某函数的每一个值
的确定性质。一类重要的逐点概念是逐点运算,这种运算是定义在函数上的运算,是将定义域上的每一点的函数值分别进行运算。
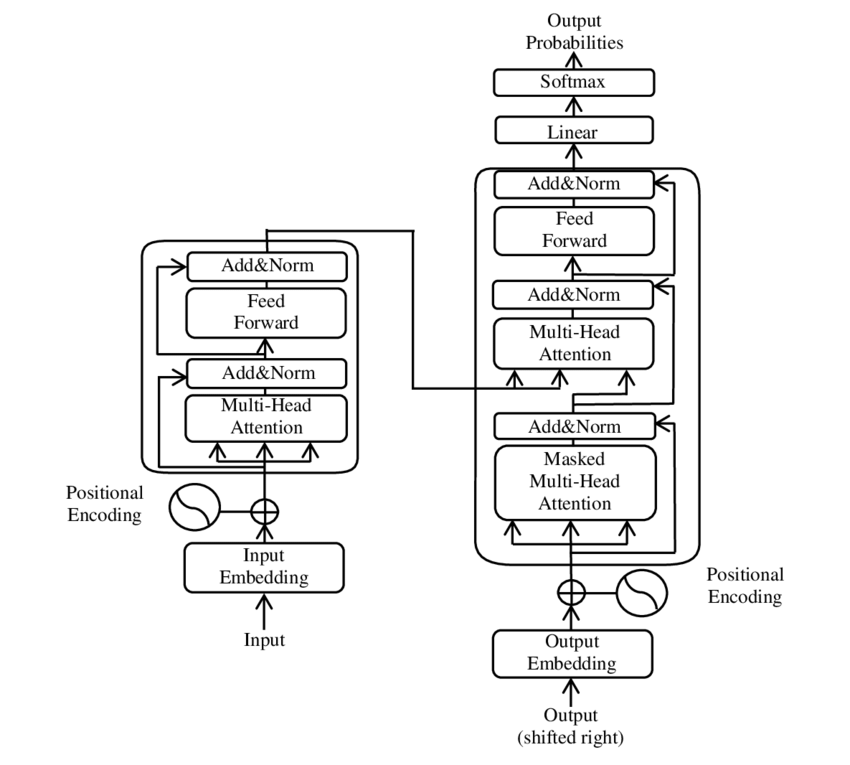
通俗的说,以论文原著中英译德机器翻译为例,在上图中,英语(神经网络的输入)从Inputs输入至编码器中,德语(神经网络的输出)从Outputs输入至解码器中,二者在解码器中进行了交叉,并促使神经网络学习英语和德语的对应关系,并输出结果(Output Probabilities)
- 基于海量的样本知识进行学习
OpenAI 在论文发表之后尝试了抛弃了编码器,做出了基于 Decoder-Only 的模型,通过将英文语句拆分为多个带有位置信息的 Token,让模型仅去考虑英文和英文之间的关注度,从而研发出了 GPT 模型
- 加入位置信息对应 Figure 1 中的 Positional Encoding这一步
- Transfomer 和 RNN 都属于序列转导模型,擅长在给定一个状态的情况下去推导出下一个状态
Encoder and Decoder Stacks
编码器:由一组
- 第一个子层是多头自注意力机制——用于捕获长距离的依赖关系
- 第二个子层是一个简单的逐位(Position-Wise)的完全连接的前馈网络——用于学习局部特征
存疑:为什么要创建残差连接和层归一化?
我们在每个子层中均创建了残差连接,并进行了层归一化(We employ a residual connection around each of
the two sub-layers, followed by layer normalization)
- 残差连接和层归一化的位置对应到 Figure 1 中的 Add & Norm 部分,详见下段
残差神经网络属于深度学习模型的一种,其核心在于让网络的每一层不直接学习预期输出,而是学习与输入之间的残差关系。这种网络通过添加“跳跃连接”,即跳过某些网络层的连接来实现身份映射,再与网络层的输出相加合并。
也就是说,每个子层的输出为
- Sublayer(x)是每个子层实现的函数,在 Figure 1 中对应 Add & Norm 前面的部分(如多头注意力和前馈网络)
- x + Sublayer(x) 对应 Figure 1 中 Add & Norm 的 Add 操作
- LayerNorm 对应 Figure 1 中 Add & Norm 的 Norm 操作
Transformer使用了和ResNet类似的残差连接,即设模块本身的映射为
,则模块输出为 。和ResNet不同,Transformer使用的归一化方法是LayerNorm。另外要注意的是,残差连接有一个要求:输入 和输出 的维度必须等长。在Transformer中,包括所有词嵌入在内的向量长度都是 。
为了实现残差连接,模型中的每个子层(包括嵌入层)都会产生维度
解码器:同样由一组
attention over the output of the encoder stack)。
和编码器类似,我们在每个子层中均创建了残差连接,并进行了层归一化
存疑:什么是the output embeddings are offset by one position
此外,我们修改了解码器中的自注意力子层,防止当前位置对后续位置的注意。通过这个Masking,结合输出嵌入层(Output Embeddings)偏移了一个位置(the output embeddings are offset by one position),保证了位置
- Mask 在解码器中用于限制注意力的范围,保证模型的自回归性质
- Mask 基于在注意力机制中引入一个矩阵参数,在矩阵中的后续位置处拥有一个近似负无穷的值,使softmax函数在计算注意力时对该处的权重近似为零
Attention
注意力函数可以被描述为将一个查询和一组键值对映射到一个输出上(mapping a query and a set of key-value pairs to an output)
- 其中,查询、键和值均为向量
存疑:什么是兼容性函数(compatibility function)
函数的输出是值的加权和
- 每个值的权重通过查询和相应的键的兼容性函数计算得出(见下节)

Scaled Dot-Product Attention
我们将这个特殊的注意力机制称为缩放点积注意力(Figure 2),输入包含查询、维度为
在数学,尤其是概率论和相关领域中,Softmax函数,或称归一化指数函数[1]:198,是逻辑斯谛函数的一种推广。它能将一个含任意实数的K维向量
“压缩”到另一个K维实向量 中,使得每一个元素的范围都在 之间,并且所有元素的和为1(也可视为一个 (k-1)维的hyperplane或subspace)。
在实践中,我们同时计算一组查询的注意力函数——将查询封装在矩阵
两种常用的注意力函数是加法注意力和点积(乘法)注意力
- 点积注意力与我们的算法唯一的区别就是缩放因子
- 加法注意力通过一个具有隐藏层的前馈网络来计算兼容性函数
- 尽管两种算法的复杂度理论上的相近的,但是由于矩阵乘法有高度优化过的代码实现,因此点积注意力在实践中要更快、更节省时间
存疑:如何定义注意力算法的优劣,通过什么测试的
尽管在
- 为了描述点积变大的原因,我们假设q和k的分量都是均值为0,方差为1的独立随机变量,那么它们的点积
的均值为0,方差为 - 分量是向量中的各个数字,如果n个数字组成了一个n维向量,那么这n个数就被称作该向量的分量
Multi-Head Attention
//TODO()
Conclusion
- 提出了新的深度学习模型 Transformer
- 摒弃了递归和卷积,完全基于注意力机制实现
- 将 encoder-decoder 架构中常用的循环层替换成为多头自注意力层